Answer:
See Below.
Explanation:
In the given trapezoid, A and B are the mid-points of QR and PR, respectively.
Question 1)
Please refer to the first diagram below.
As instructed, we will join Q and B to produce QB to meet SR at C.
Statements: Reasons:
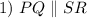 Given
Given
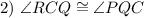 Alternate Interior Angles Theorem
Alternate Interior Angles Theorem
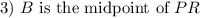 Given
Given
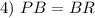 Definition of Midpoint
Definition of Midpoint
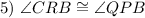 Alternate Interior Angles Theorem
Alternate Interior Angles Theorem
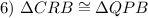 AAS-Congruence
AAS-Congruence
 CPCTC
CPCTC
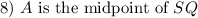 Given
Given
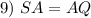 Definition of Midpoint
Definition of Midpoint
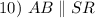 Triangle Midsegment Theorem
Triangle Midsegment Theorem
Question 2)
(We will use the proven statements above as "given.")
(And please continue referring to the first figure provided.)
Statements: Reasons:
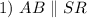 Given
Given
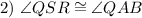 Corresponding Angles Theorem
Corresponding Angles Theorem
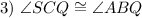 Corresponding Angles Theorem
Corresponding Angles Theorem
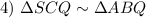 Angle-Angle Similarity
Angle-Angle Similarity
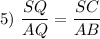 CSSTP
CSSTP
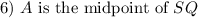 Given
Given
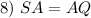 Definition of Midpoint
Definition of Midpoint
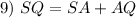 Segment Addition
Segment Addition
 Substitution
Substitution
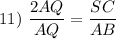 Substitution
Substitution
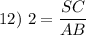 Division Property of Equality
Division Property of Equality
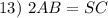 Multiplication Property of Equality
Multiplication Property of Equality
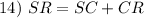 Segment Addition
Segment Addition
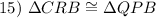 Given
Given
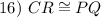 CPCTC
CPCTC
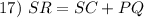 Substitution
Substitution
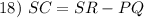 Subtraction Property of Equality
Subtraction Property of Equality
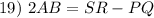 Substitution
Substitution
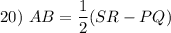 Division Property of Equality
Division Property of Equality