Answer:
(a)
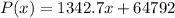
(b)
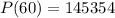
(c)
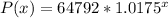
(d)
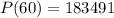
(e) The exponential model is more realistic
Explanation:
Given
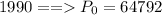
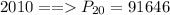
Solving (a): The linear model of the population growth
First, we calculate the slope of the function.
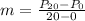
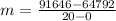
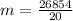
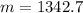
The linear equation is then calculated using:
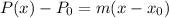
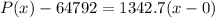
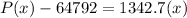
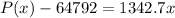
Make P(x) the subject
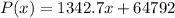
Solving (b): The population in 2050
First, calculate x:
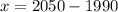
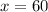
Substitute 60 for x in
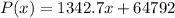

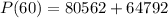
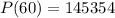
The population in 2050 is 145354
Solving (c): The exponential model of the population growth
An exponential model is:
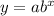
In this case, it is:

For x = 20, we have:
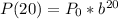
Substitute values for P(20) and P0
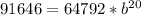
Divide both sides by 64792
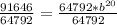
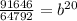
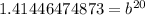
Take the 20th root of both sides
![\sqrt[20]{1.41446474873} = b](https://img.qammunity.org/2022/formulas/mathematics/high-school/loiq5l7s1l6pbz5xcrlzwtwgewkw3pd57i.png)
![b = \sqrt[20]{1.41446474873}](https://img.qammunity.org/2022/formulas/mathematics/high-school/jx1n3iu3q9au22q481quztrql4aoqu9wtf.png)
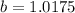
So, the model is:

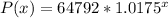
Solving (d): The population in 2050
First, calculate x:
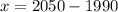
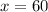
Substitute 60 for x in
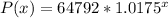
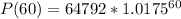
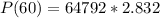
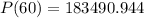
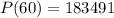 ---- approximated
---- approximated
(e) The most realistic model
The exponential model is more realistic. This is so because:
The linear model grows at a constant linear rate which means that, every year a certain amount of individuals is added to the society. However, this is not always so because it is almost impossible to for growth rate to be constant
A curve in the exponential model shows that the addition of individuals in the society every year is not always constant.