Question

QUESTION

Jaya had rupees 220 in her purse.
They were in five-rupee rupee, ten-rupee and 2 rupee notes.
She had 6 ten-rupee notes more than that of the five rupee notes.
And she had 5 two-rupee notes.
How many five-rupee and ten-rupee notes did she have?

Answer 1

Jaya had 10 five-rupee notes and 16 ten-rupee notes.

Step-by-step explanation:

Let's solve this problem step by step:

1. Let the number of five-rupee notes be x.
2. The number of ten-rupee notes is 6 more than the number of five-rupee notes, so it is x + 6.
3. The total value of the five-rupee notes is 5x rupees, and the total value of the ten-rupee notes is 10(x + 6) rupees.
4. She also has 5 two-rupee notes, which have a total value of 5 * 2 = 10 rupees.
5. According to the problem, the total value of all the notes is 220 rupees. So, we can write the equation: 5x + 10(x + 6) + 10 = 220.
6. Simplifying the equation: 5x + 10x + 60 + 10 = 220. Combining the x terms and simplifying further: 15x + 70 = 220.
7. Subtracting 70 from both sides of the equation: 15x = 150.
8. Dividing both sides of the equation by 15 to solve for x: x = 10.

So, Jaya had 10 five-rupee notes and 10 + 6 = 16 ten-rupee notes.

Answer 2

No. of five-rupee note: 10

No. of ten-rupee note: 16

Step-by-step explanation:

Let's denote the number of five-rupee notes as
`\sf x`, the number of ten-rupee notes as
`\sf y`, and the number of two-rupee notes as
`\sf z`.

According to the given information:

• The total value of five-rupee notes is
  `\sf 5x` rupees.
• The total value of ten-rupee notes is
  `\sf 10y` rupees.
• The total value of two-rupee notes is
  `\sf 2z` rupees.

Jaya had a total of 220 rupees, so we can write the equation:

`\sf 5x + 10y + 2z = 220`

Now, we are given two additional pieces of information:

• She had 6 ten-rupee notes more than the five-rupee notes, which can be expressed as
  `\sf y = x + 6`.
• She had 5 two-rupee notes, which can be expressed as
  `\sf z = 5`.

Now, we have a system of three equations:

`\sf \begin{aligned}5x + 10y + 2z &= 220 \\y &= x + 6 \\z &= 5\end{aligned}`

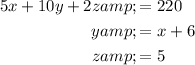
Substitute the value of
`\sf z` into the first equation:

`\sf 5x + 10y + 2(5) = 220`

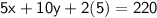
Simplify:

`\sf 5x + 10y + 10 = 220`

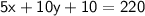
Subtract 10 from both sides:

`\sf 5x + 10y + 10 -10= 220-10`

`\sf 5x + 10y = 210`

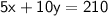
Now, substitute the value of
`\sf y` from the second equation into this new equation:

`\sf 5x + 10(x + 6) = 210`

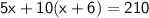
Distribute:

`\sf 5x + 10x + 60 = 210`

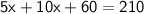
Combine like terms:

`\sf 15x + 60 = 210`

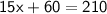
Subtract 60 from both sides:

`\sf 15x + 60-60 = 210-60`

`\sf 15x = 150`

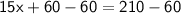
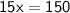
Divide by 15:

`\sf (15x)/(15)=(150)/(15)`

`\sf x = 10`

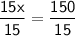
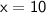
Now that we have the value of
`\sf x`, substitute it back into the equation for
`\sf y`:

`\sf y = x + 6 = 10 + 6 = 16`

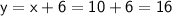
So, Jaya has 10 five-rupee notes and 16 ten-rupee notes.