Answer:
Approximately
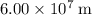 .
.
Step-by-step explanation:
The magnitude
 of the gravitational attraction between two objects in space is:
of the gravitational attraction between two objects in space is:
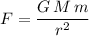 ,
,
Where:
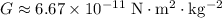 is the gravitational constant,
is the gravitational constant,
 and
and
 are the mass of the two objects, and
are the mass of the two objects, and
 is the distance between the center of mass of the two objects.
is the distance between the center of mass of the two objects.
In this question,
 ,
,
 , and the magnitude of the gravitational attraction are given. Rearrange the equation above to find an expression for distance
, and the magnitude of the gravitational attraction are given. Rearrange the equation above to find an expression for distance
 :
:
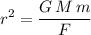 .
.
 .
.
Substitute
 and
and
 into the expression:
into the expression:
 .
.
In other words, the distance between the center of mass of this planet and its moon would be approximately
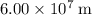 .
.