Question

Find the coordinates of the turning point when y=5x^3 - 6x^2 - 4X + 8

Answer 1

Given:

The equation is

`y=5x^3-6x^2-4x+8`

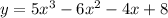
To find:

The coordinates of the turning point.

Solution:

We have,

`y=5x^3-6x^2-4x+8`

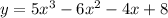
Differentiate with respect to x.

`(dy)/(dx)=5(3x^2)-6(2x)-4(1)+(0)`

`(dy)/(dx)=15x^2-12x-4`

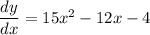
For the turning points
`(dy)/(dx)=0`.

`15x^2-12x-4=0`

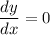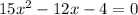
Using quadratic formula:

`x=(-b\pm √(b^2-4ac))/(2a)`

`x=(-(-12)\pm √((-12)^2-4(15)(-4)))/(2(15))`

`x=(12\pm √(144+240))/(30)`

`x=(12\pm √(384))/(30)`

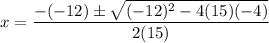
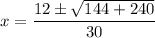
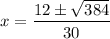
Now,

`x=(12+√(384))/(30)\text{ and }x=(12-√(384))/(30)`

`x\approx 1.053\text{ and }x\approx-0.253`

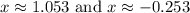
Putting x=1.053 in the given equation, we get

`y=5(1.053)^3-6(1.053)^2-4(1.053)+8`

`y\approx 2.973`

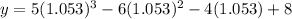
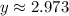
Putting x=−0.253 in the given equation, we get

`y=5(-0.253)^3-6(-0.253)^2-4(-0.253)+8`

`y\approx 8.547`

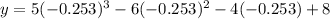
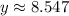
Therefore, the turning points are (1.053,2.973) and (-0.253, 8.547).