Question

PLEASE HELP ME ASAP I NEED THEM IN THE NEXT 5 MINUTES

Answer 1

`A(\triangle ABC) = 7.2\: units^2`

Explanation:

C = (0, 7)

Since, point A lies in y-axis, so it's x coordinate will be zero. Line y = 2x + 1 passes through point A.

Therefore, plug x = 0 in y = 2x +1, we find:

y = 2*0 + 1 = 0 + 1 = 1

Hence, coordinates of point A are (0, 1).

Now, by distance formula:

`AC= √((0-0)^2 +(7-1)^2)`

`AC= √((0)^2 +(6)^2 )`

`AC= √(0 +36 )`

`AC= √(36 )`

`AC= 6\: units`

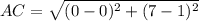
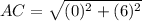
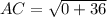
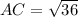
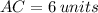
Length of perpendicular CB dropped from point C (0, 7) to line y = 2x + 1 or 2x - y + 1 = 0 can be obtained as given below:

`CB =\frac2* 0+(-1)* 7+1{\sqrt {2^2 +(-1)^2} }`

`CB =\frac0-7+1{\sqrt {4 +1} }`

`CB =\frac{\sqrt {5} }`

`CB =(6)/(2.24)`

`CB =2.68\: units`

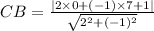
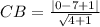
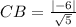
By Pythagoras Theorem:

`AB=√(AC^2 - CB^2)`

`AB=√(6^2 - (2.68)^2)`

`AB=√(36 - 7.18)`

`AB=√(28.82)`

`AB=5.36842621\: units`

`AB\approx 5.37\: units`

`A(\triangle ABC) = (1)/(2) * AB* CB`

`A(\triangle ABC) = (1)/(2) * 5.37* 2.68`

`A(\triangle ABC) = (1)/(2) * 14.3916`

`A(\triangle ABC) = 7.1958`

`A(\triangle ABC) = 7.2\: units^2`

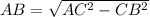
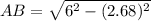
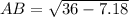
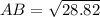
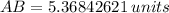
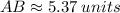
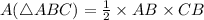
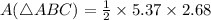
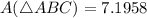
Hope it be correct.