Question

Plz solve it and help me for it​

Answer 1

Given:

Base angle of an isosceles triangle is 15 degrees more than its vertical angle.

To find:

The measure of each angle of the triangle.

Solution:

Let x be the vertical angle. Then,

One base angle = x+15 degrees

We know that base angles of an isosceles triangle are equal.

Another base angle = x+15 degrees

Now, the sum of all angles of a triangle is 180 degrees by the angle sum property.

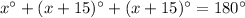`x^\circ+(x+15)^\circ+(x+15)^\circ=180^\circ` (Angle sum property)

`(3x+30)^\circ=180^\circ`

`3x+30=180`

`3x=180-30`

`3x=150`

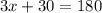
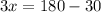
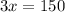
Divide both sides by 3.

`x=(150)/(3)`

`x=50`

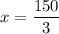
The measure of base angles is

`(x+15)^\circ=(50+15)^\circ`

`(x+15)^\circ=65^\circ`

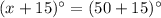
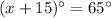
Therefore, the measure of angles are 50°, 65° and 65°.