Question

The tables of ordered pairs represent some points on the graphs of lines m and n.

Which system of equations represents lines m and n?
Select two correct answers.

Answer 1

The system of equations that represents lines m and n is: B. y = -2x + 5 and D. y = 2.25x - 7.

How to write the system of equations?

Using any two set of ordered pairs from each table, write the equation of each line as explained below:

To find the equation for the line passing through the points
`(x_1, y_1) = (4, 2)` and
`(x_2, y_2) = (8, 11)`, you can use the point-slope form of the equation for a line:

`y - y_1 = m(x - x_1)`

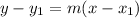
Substitute:

`m = \frac{{11 - 2}}{{8 - 4}} = (9)/(4)`

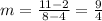
Now, plug in the slope and one set of coordinates into the point-slope form:

y - 2 = 9/4(x - 4)

Simplify the equation:

4y - 8 = 9(x - 4)

4y - 8 = 9x - 36

4y = 9x - 28

y = 2.25x - 7 (equation of one line)

For the second line, points
`(x_1, y_1)` = (-1, 7) and
`(x_2, y_2)` = (2, 1), you can follow the same process:

`m = \frac{{1 - 7}}{{2 - (-1)}} = (-6)/(3) = -2`

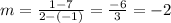
Substitute the slope and one point:

y - 7 = -2(x - (-1))

Simplify the equation:

y - 7 = -2x - 2

y = -2x + 5 (equation of the second line).

Thus, the answer is:

B. y = -2x + 5 and D. y = 2.25x - 7