Question

B. Translate each statement to an equation using k as the constant of variation.

1. m varies directly to a.
2. p varies inversely as q.
3. r varies directly as s and inversely as t.
4. z varies jointly as e and f.
5. F varies directly as the square of t.
6. The distance (d) traveled by a car varies jointly as the rate (r) and the time (t) of travel.
7. The air pressure (P) in inversely proportional to the altitude (h).
8. The amount of water pressure (P) in a closed container varies directly as the volume (V) of the
water.
9. The distance (d) of a falling body varies directly as the square of the time (t) traveled.
1
10. The stiffness (s) of a beam varies jointly as its breadth (b) and depth (d) and inversely as the
square
of its length (L).
2​

Answer 1

See Explanation

Explanation:

To do this, we will make use of the following rules:

Direct Variation:
`a\ \alpha\ b` =>
`a = kb`

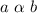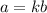
Inverse Variation:
`a\ \alpha\ (1)/(b)` ==>
`a = k/b`

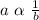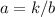
Joint Variation:
`a\ \alpha\ bc` ==>
`a= kbc`

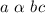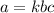
Direct, then inverse variation:
`a\ \alpha\ b\ \alpha\ (1)/(c)` ==>
`a= kb/c`

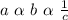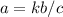
Having highlighted the rules, the solution is as follows:

1. m varies directly to a

`m\ \alpha\ a`

`m =ka`

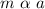
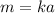
2. p varies inversely as q.

`p\ \alpha\ (1)/(q)`

`p\ = k(1)/(q)`

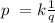
3.
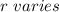`r\ varies` directly as s and inversely as t.

`r\ \alpha\ s\ \alpha\ (1)/(t)`

`r = k(s)/(t)`

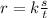
4. z varies jointly as
`e\ and\ f.`

`z\ \alpha \ ef`

`z = kef`

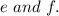
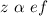
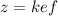
5. F varies directly as the
`square\ of\ t.`

`F\ \alpha\ t^2`

`F = kt^2`

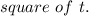
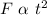
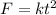
6. d varies jointly r and t

`d\ \alpha\ rt`

`d = krt`

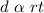
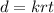
7. P is inversely proportional to h.

`P\ \alpha\ (1)/(h)`

`P= (k)/(h)`

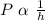
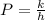
8. P varies directly as V

`P\ \alpha\ V`

`P=kV`

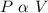
9. d varies directly as the square of t

`d\ \alpha\ t^2`

`d = kt^2`

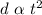
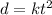
10. s varies jointly as b and d and inversely as the square L

`s\ \alpha\ bd\ \alpha\ (1)/(L^2)`

`s = k(bd)/(L^2)`