Question

The graph of

\[y=g(x)\] is a transformation of the graph of
\[y=h(x)\].
Two congruent parabolas labeled g of x and h of x on an x y coordinate plane. The x- and y- axes scale by one. The graph labeled h of x has a vertex at (four, two) and has an interval of decrease from one to four and an interval of increase from four to seven. The graph labeled g of x has a vertex at (negative six, negative six) and has an interval of decrease from negative ten to negative six and an interval of increase from negative six to negative two.
\[\small{1}\]
\[\small{2}\]
\[\small{3}\]
\[\small{4}\]
\[\small{5}\]
\[\small{6}\]
\[\small{7}\]
\[\small{8}\]
\[\small{9}\]
\[\small{\llap{-}2}\]
\[\small{\llap{-}3}\]
\[\small{\llap{-}4}\]
\[\small{\llap{-}5}\]
\[\small{\llap{-}6}\]
\[\small{\llap{-}7}\]
\[\small{\llap{-}8}\]
\[\small{\llap{-}9}\]
\[\small{1}\]
\[\small{2}\]
\[\small{3}\]
\[\small{4}\]
\[\small{5}\]
\[\small{6}\]
\[\small{7}\]
\[\small{8}\]
\[\small{9}\]
\[\small{\llap{-}2}\]
\[\small{\llap{-}3}\]
\[\small{\llap{-}4}\]
\[\small{\llap{-}5}\]
\[\small{\llap{-}6}\]
\[\small{\llap{-}7}\]
\[\small{\llap{-}8}\]
\[\small{\llap{-}9}\]
\[y\]
\[x\]
\[\blue{y=h(x)}\]
\[\purple{y=g(x)}\]
Two congruent parabolas labeled g of x and h of x on an x y coordinate plane. The x- and y- axes scale by one. The graph labeled h of x has a vertex at (four, two) and has an interval of decrease from one to four and an interval of increase from four to seven. The graph labeled g of x has a vertex at (negative six, negative six) and has an interval of decrease from negative ten to negative six and an interval of increase from negative six to negative two.
Given that
\[h(x)=(x-4)^2+2\], write an expression for
\[g(x)\] in terms of
\[x\].
\[g(x)= \]

Answer 1

Since
`h(x) = (x - 4)^2 - 2`, an expression for g(x) in terms of x is
`g(x) = (x +6)^2 - 6`.

In Mathematics, a translation is a type of transformation that shifts every point of a geometric object in the same direction on the cartesian coordinate, and for the same distance.

Based on the information provided in the diagram, we have the following coordinates:

(x, y) → (x - h, y - k)

(-6, -6) → (4, 2).

4 = x - h

4 = -6 - h

h = -6 - 4

h = -10 (10 units left)

2 = y + k

2 = -6 + k

k = 6 - 2

k = 4 (4 units down).

In conclusion, a horizontal translation 10 units to the left and 4 units down would map the parent quadratic function h(x) to the transformed quadratic function g(x);

g(x) = h(x + 10) - 4

`g(x) = (x -4+10)^2 - 2-4 \\\\g(x) = (x +6)^2 - 6`

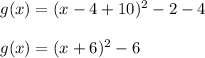
Complete Question:

The graph of y = g(x) is a transformation of the graph of y = h(x).

Given that
`h(x) = (x - 4)^2 - 2`, write an expression for g(x) in terms of x.