The function for the distance of the car from the stop sign can be used to find the graph of the relationship and the average rate of change of the distance as follows;
a. The graph of the relationship between the distance from the stop sign and the number of seconds, created with MS Excel is attached
b. The average rate of change in the interval 0 ≤ x ≤ 2 is 0.625, which represents the average speed of the car in the first two seconds
The details of the steps used to evaluate the function can be presented as follows;
a. Please find attached the graph of the relationship between the distance of the car from the stop sign and the number of seconds, created with MS Excel
b. The distance of the car from the stop sign at t = 0, f(0) is; 1.5⁰ = 1
The distance of the car from the stop sign at t = 2, f(2) is; 1.5² = 2.25
The average rate of change of the distance in the interval 0 ≤ t ≤ 2, therefore is; (f(2) - f(0))/(2 - 0)
(f(2) - f(0))/(2 - 0) = (2.25 - 1)/(2 - 0)
(2.25 - 1)/(2 - 0) = 0.625
The average rate of change of the distance of the car from the stop sign in the interval 0 ≤ t ≤ 2, is 0.625 ft/s
The average rate of change indicates that the average speed of the car in the interval is about 0.625 ft/s
The possible complete question, obtained from a similar question found through search can be presented as follows;
f(t) =
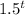 , with d = f(t), represents a car's distance d (measured in feet) from a stop sign in terms of the number of seconds t since the car started to move away from the stop sign
, with d = f(t), represents a car's distance d (measured in feet) from a stop sign in terms of the number of seconds t since the car started to move away from the stop sign
a. Sketch a graph of this relationship. Be sure to label your axis
b. Determine the average rate of change of the distance of the car from the stop sign on the following intervals, then provide more light on how to interpret each value
0 ≤ t ≤ 2