Given:
The expression is
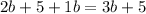
To find:
Whether the two expression in the equation are equal or equivalent.
Solution:
If two expression are exactly the same, then they are equal and if the two expressions are different but the after simplification both are same, then they are called equivalent expressions.
We have,
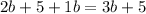
Taking LHS, we get
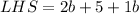
On combining liker terms, we get
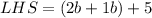

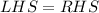
In the given equation both expression are different but after simplification LHS = RHS, therefore the expression are equivalent not equal.