Question

14. A right cone has a height of 14 in and a base diameter of 17 in.

a Sketch and label a diagram of the cone
b. Determine the area of the lateral surface of the cone, to the nearest square inch​

Answer 1

Given:

The height of a right cone = 14 in

Base diameter = 17 in

To find:

The diagram of the cone and its lateral surface area.

Solution:

(a)

The diagram of a right cone with height 14 in and base diameter of 17 in is shown below.

Diagram is not to scale.

(b)

We know that lateral surface of the cone is

`A=\pi rl`

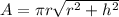`A=\pi r√(r^2+h^2)` ...(i)

Where, r is the base radius, h is vertical height and l is the slant height of the cone.

Base radius of the cone =
`\frac{\text{Base diameter}}{2}`

`r=(17)/(2)`

`r=8.5`

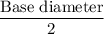
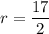
Now,

Putting r=8.5, h=14 and π=3.14 in (i), we get

`A=(3.14)(8.5)√((8.5)^2+(14)^2)`

`A=26.69√(72.25+196)`

`A=26.69√(268.25)`

`A=437.1379`

`A\approx 437`

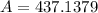
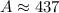
Therefore, the lateral surface area of the cone is 437 sq. inches.