Question

In parallelogram ABCD, base AD is 15 and side AB is 8. What are the height and area of paralelogram ABCD if mDAB is 20?

Answer 1

Explanation:

✰
`\underline{ \underline{ \large{ \tt{G\: I \: V \: E \: N}}}} :`

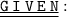
• AD = 15 , AB = 8 ,
  `\angle` DAB

✰
`\underline{ \underline{ \large{ \tt{T \: O \: \: F\: I \: N \: D}}}} :`

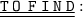
• Height & Area of the given parallelogram

✰
`\underline{ \underline{ \large{ \tt{S \: O</p><p> \: L \: U \: T\: I\: O \: N}}}} :`

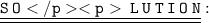
In right angled triangle ABE :

• Hypotenuse ( h ) = 8
• Perpendicular ( p ) = h [ height ]
• 
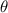  `\theta` = 20°

Now , Using trigonometric ratio :

`\large{ \tt{Sin \theta \: = \: (Perpendicular)/(Hypotenuse) }}`

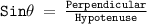
Plug the known values :

⟶
`\large{ \tt{ Sin(20) = (h)/(8) }}`

⟶
`\large{ \tt{0.34 = (h)/(8)}}`

⟶
`\large{ \tt{h = 0.34 * 8}}`

⟶
`\large{ \tt{h = 2.72}}`

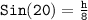
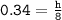
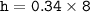
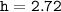
Now , We have :

• Base ( b ) = 15
• Height ( h ) = 2.72

Finding the area of a parallelogram whose base and height are 15 and 2.72 respectively :

❀
`\underline{ \underline{ \text{Area \: of \: parallelogram = \tt{b *\: h}}}}`

⟶
`\large{ \tt{A = 15 *2.72}}`

⟶
`\large{ \tt{A = 40.8 \: {units}^(2) }}`

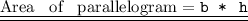
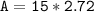
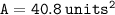
Hence , Our final answer :

`\large{ \boxed{ \sf{Height \: ( \: h \: ) = 2.72 \: units}}}`

`\large{ \boxed{ \sf{Area \: of \: parallelogram \: ( \:A \: ) = \: 40.8 \: {units}^(2) }}}`

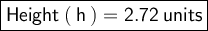
Hope I helped ! ♡

Have a wonderful day / night ! ツ

#
`\underbrace{ \tt{Carry \: On \: Learning}}` !! ✎

▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁