Answer:
x = - 44
Explanation:
the equation of a line in slope- intercept form is
y = mx + c ( m is the slope and c the y- intercept )
given
2x - 10y = 18 ( subtract 2x from both sides )
- 10y = - 2x + 18 ( divide through by - 10 )
y =
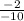 x +
x +
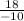 , that is
, that is
y =
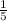 x -
x -
 ← in slope- intercept form
← in slope- intercept form
with slope m =
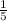
given a line with slope m then the slope of a line perpendicular to it is
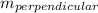 = -
= -
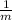 = -
= -
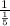 = - 5
= - 5
calculate the slope of the line through the 2 given points and equate to - 5
calculate slope m using slope formula
m =
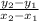
with (x₁, y₁ ) = (- 3, 6 ) and (x₂, y₂ ) = (7, x )
m =
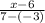 =
=
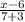 =
=
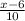
then equating
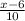 = - 5 ( multiply both sides by 10 to clear the fraction )
= - 5 ( multiply both sides by 10 to clear the fraction )
x - 6 = - 50 ( add 6 to both sides )
x = - 44