Answer:
Domain: all real numbers x except x = -4

Explanation:
Given function:
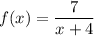
The domain of a function is the set of all possible input values (x-values).
When the denominator of a rational function is zero, the function is undefined.
To find the value(s) of x for which the function is undefined, set the denominator to zero and solve for x:
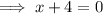
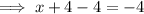
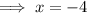
Therefore, the domain of the given function is:
- all real numbers x except x = -4
The vertical asymptote(s) of a rational function are the values of x for which the denominator is zero.
Therefore, there is a vertical asymptote at x = -4.
As x gets very close to x = -4 from the negative side, the function approaches -∞ because the denominator will be an extremely small negative number.
As x gets very close to x = -4 from the positive side, the function approaches ∞ because the denominator will be an extremely small positive number.
Therefore, the behaviour of the function near the excluded x-value is: