Answer:
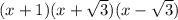
Explanation:
We need to factor out ,
![\longrightarrow x^3 + x^2 -3x -3 = p(x) \ \ \rm[say]\\](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/mahu7tyml885zxmb6p60.png)
Look out for factors of 3 , which could be , ±1 or ±3 . That is : 1 , -1 , 3 , -3
Substitute these factors one by one in the given cubic polynomial and look out for that value for which the expression becomes 0 .
Substitute
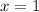 ,
,
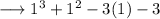
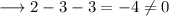
Again substitute
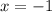 , we have ;
, we have ;
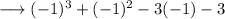
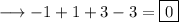
This implies
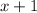 is a factor of the given cubic polynomial. Now on dividing the polynomial by
is a factor of the given cubic polynomial. Now on dividing the polynomial by
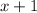 , we have; ( see attachment)
, we have; ( see attachment)
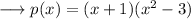
Now we can further factorise
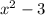 as ,
as ,
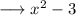
can be written as ,
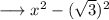
on using identity
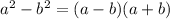 , we have;
, we have;
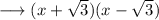
So the final factorised form of the given cubic polynomial is ,
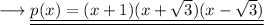
and we are done!