Question

Factor x³ + x² − 3x − 3.

Answer 1

(x^2-3)(x+1)

Explanation:

we can split this into 2 equations

x^3+x^2

-3x-3

first one we can take x^2 out of the equations

x^2(x+1)

second one we can take out -3 of the equation

-3(x+1)

now we can combine them

(x^2-3)(x+1)

hopes this helps

Answer 2

`(x+1)(x+\sqrt3)(x-\sqrt3)`

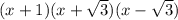
Explanation:

We need to factor out ,

`\longrightarrow x^3 + x^2 -3x -3 = p(x) \ \ \rm[say]\\`

Look out for factors of 3 , which could be , ±1 or ±3 . That is : 1 , -1 , 3 , -3

Substitute these factors one by one in the given cubic polynomial and look out for that value for which the expression becomes 0 .

Substitute
`x = 1` ,

`\longrightarrow 1^3 + 1^2 -3(1) -3 \\`

`\longrightarrow 2 -3-3 = -4 \\eq 0\\`

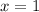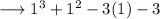
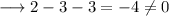
Again substitute
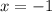`x = -1` , we have ;

`\longrightarrow (-1)^3+(-1)^2-3(-1)-3\\`

`\longrightarrow -1 + 1 +3 - 3 = \boxed{0 } \\`

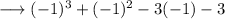
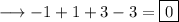
This implies
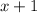`x +1` is a factor of the given cubic polynomial. Now on dividing the polynomial by
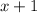`x +1` , we have; ( see attachment)

`\longrightarrow p(x) = (x+1)(x^2-3)\\`

Now we can further factorise
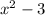`x^2-3` as ,

`\longrightarrow x^2 - 3 \\`

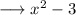
can be written as ,

`\longrightarrow x^2-(\sqrt3)^2 \\`

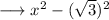
on using identity
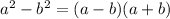`a^2-b^2=(a-b)(a+b)` , we have;

`\longrightarrow (x+\sqrt3)(x-\sqrt3) \\`

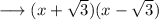
So the final factorised form of the given cubic polynomial is ,

`\longrightarrow \underline{\underline{ p(x)= (x+1)(x+\sqrt3)(x-\sqrt3)}} \\`

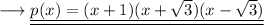
and we are done!