Mathematical induction is a proof technique where we establish a base case and then show that if the statement holds for an arbitrary value, it also holds for the next value. In this case, we want to prove that the product of any
 consecutive positive integers is divisible by
consecutive positive integers is divisible by
 .
.
Base Case
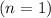 : When
: When
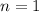 , the product of a single positive integer is itself, and
, the product of a single positive integer is itself, and
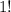 is also 1. Therefore, the base case holds true.
is also 1. Therefore, the base case holds true.
Inductive Step: Assume that the product of
 consecutive positive integers is divisible by
consecutive positive integers is divisible by
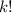 for some arbitrary
for some arbitrary
 .
.
Now, we want to show that the product of
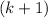 consecutive positive integers is divisible by
consecutive positive integers is divisible by
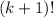 . We use the provided identity:
. We use the provided identity:
![\[ (m(m + 1) \cdots (m + k))/(k!) = ((m-1)m(m + 1) \cdots (m + k - 1))/((k-1)!) + (m(m + 1) \cdots (m + k - 1))/(k!) \]](https://img.qammunity.org/2024/formulas/mathematics/college/rvmpuwjsmwyomi72rov9rhlcukfo6wu06w.png)
This identity allows us to express the product of
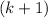 consecutive integers as the sum of two terms, each of which is divisible by
consecutive integers as the sum of two terms, each of which is divisible by
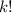 .
.
By the inductive assumption, both terms are divisible by
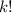 , and hence their sum, representing the product of
, and hence their sum, representing the product of
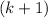 consecutive positive integers, is also divisible by
consecutive positive integers, is also divisible by
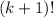 .
.
Thus, by mathematical induction, we have shown that the product of any
 consecutive positive integers is divisible by
consecutive positive integers is divisible by
 .
.