Answer:
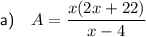
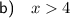
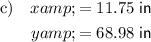
Explanation:
Part (a)
Print area (blue rectangle):
- width = (x - 4) in
- length = (y - 2) in
- area = 30 in²
Create an equation for the print area using the given values and rearrange to isolate y:
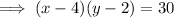
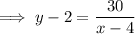

Total area of the page is:

Substitute the found expression for y to write an equation for the total area of the page in terms of x:

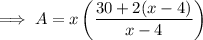
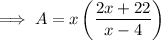
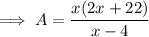
Part (b)
If x < 4 then A < 0.
If x = 4 then A is undefined.
Therefore, given the physical constraints of the problem, x has to be greater than 4.
Part (c)
Using a graphing utility, graph the function for area from part (a) when x > 4 (see attachment). (Note: The x-axis of the attached graph crosses the y-axis at y = 50 for ease of inspection).
The values of x and y that use the least amount of paper are the coordinates of the minimum point of the graph.
From inspection of the graph, the minimum point is: