Question

Help me find the missing number please !! hurry also i have to turn this in tomorrow !!

Answer 1

The length of cuboid is
`\sf{7(1)/(5) \: in}`

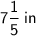
Explanation:

Here's the required formula to find the length of cuboid :

`\longrightarrow{\pmb{\sf{V = \ell * w * h}}}`

• 
  `\pink\star` V = Volume
• 
  `\pink\star` l = length
• 
  `\pink\star` w = width
• 
  `\pink\star` h = height

Substituting all the given values in the formula to find the length of cuboid :

• 
  `\purple\star` V = 60
• 
  `\purple\star` l = ?
• 
  `\purple\star` w = 2½
• 
  `\purple\star` h = 3⅓

`\implies{\sf{V = \ell * w * h}}`

`\implies{\sf{60= \ell* 2(1)/(2) * 3(1)/(3)}}`

`\implies{\sf{60= \ell* (4 + 1)/(2) * (9 + 1)/(3)}}`

`\implies{\sf{60= \ell* (5)/(2) * (10)/(3)}}`

`\implies{\sf{60= \ell* (5 * 10)/(2 * 3)}}`

`\implies{\sf{60= \ell* (50)/(6)}}`

`\implies{\sf{\ell = 60 * (6)/(50)}}`

`\implies{\sf{\ell = (60 * 6)/(50)}}`

`\implies{\sf{\ell = (360)/(50)}}`

`\implies{\sf{\ell = \frac{36 \cancel{0}}{5 \cancel{0}}}}`

`\implies{\sf{\ell = (36)/(5)}}`

`\implies{\sf{\ell = 7(1)/(5)}}`

`\star{\underline{\boxed{\tt{\red{\ell = 7(1)/(5) \: in}}}}}`

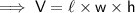
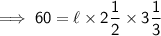
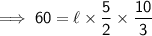
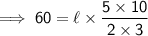
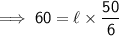
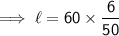
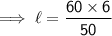
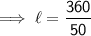
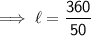
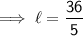
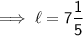
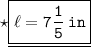
Hence, the length of cuboid is 7(1/5) in.

`\rule{300}{2.5}`