The volume of the empty space inside Container A is approximately 298.5 cubic feet (rounded to the nearest tenth).
The volume V of a cylinder is given by the formula

For Container A:
![\[ V_A = \pi * (4^2) * 11 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/4v7905324plolv0x3z1bjjrrarrdm3qx9x.png)
For Container B:
![\[ V_B = \pi * (3^2) * 18 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/1crprg4ntov2g9w0rlrcrupuoycr0uaat5.png)
Now, calculate the volumes:
![\[ V_A \approx 452.38934 \text{ cubic feet} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/6v8x3wav8td5amul22p4nsv8bmqm4gvdj6.png)
![\[ V_B \approx 153.93804 \text{ cubic feet} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/zw3b1t4336y6ddone4vpzm2p6ntjmzziqk.png)
The empty space inside Container A is then the difference:
Empty space} =
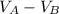
Empty space
Empty space
 cubic feet
cubic feet
So, the volume of the empty space inside Container A is approximately 298.5 cubic feet (rounded to the nearest tenth).