The total interest Niki have paid is $10,294.26. The correct option is B.
To find the total interest paid by Niki on his $61,600 loan with an interest rate of 9.84%, compounded every two months over eleven years, we can use the compound interest formula:
![\[ A = P \left(1 + (r)/(n)\right)^(nt) \]](https://img.qammunity.org/2024/formulas/business/high-school/uotb50mnfel9dwecmb8uu95z6g2hl2eej6.png)
Where:
-
 is the total amount after time
is the total amount after time
 ,
,
-
 is the principal amount (initial loan amount),
is the principal amount (initial loan amount),
-
 is the annual interest rate (in decimal form),
is the annual interest rate (in decimal form),
-
 is the number of times interest is compounded per year,
is the number of times interest is compounded per year,
-
 is the time in years.
is the time in years.
The total interest paid
 is then given by
is then given by
 .
.
Given that the loan is compounded every two months,
 (since there are 12 months in a year), and the interest rate is 9.84% or
(since there are 12 months in a year), and the interest rate is 9.84% or
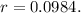
![\[ A = 61600 \left(1 + (0.0984)/(6)\right)^(6 * 11) \]](https://img.qammunity.org/2024/formulas/mathematics/college/28c95zlis30wgtgs736nawsflwevsu94wj.png)
Calculate A and then find I by subtracting the principal $61,600. Round the answer to the nearest cent.
After calculations, the correct answer is:
b. $10,294.26