The correct option is a. Card Q’s balance increased by $7.22 more than Card P’s balance.
To determine which card's balance will have increased more after four years, we can use the compound interest formula:
![\[ A = P \left(1 + (r)/(n)\right)^(nt) \]](https://img.qammunity.org/2024/formulas/business/high-school/uotb50mnfel9dwecmb8uu95z6g2hl2eej6.png)
Where:
-
 is the total amount after time
is the total amount after time
 ,
,
-
 is the principal amount (initial balance),
is the principal amount (initial balance),
-
 is the annual interest rate (in decimal form),
is the annual interest rate (in decimal form),
-
 is the number of times interest is compounded per year,
is the number of times interest is compounded per year,
-
 is the time in years.
is the time in years.
For Card P:
![\[ A_P = 726.19 \left(1 + (0.1019)/(2)\right)^(2 * 4) \]](https://img.qammunity.org/2024/formulas/mathematics/college/2wfkxxa9xoj6dzho31sgjwgpbrw25iy0uz.png)
For Card Q:
![\[ A_Q = 855.20 \left(1 + (0.0863)/(12)\right)^(12 * 4) \]](https://img.qammunity.org/2024/formulas/mathematics/college/mcbii0tmhb4nlxzh2ciqf34zfyowoj3a61.png)
Calculate both
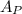 and
and
 and find the difference
and find the difference

After calculations, the correct answer is:
a. Card Q's balance increased by $7.22 more than Card P's balance.