Question

Defining a Piecewise Function

On a coordinate plane, a piecewise function has 2 lines. The first line has an open circle at (0, 1) and goes up through (negative 4, 3) with an arrow instead of an endpoint. The second line has a closed circle at (0, negative 2) and goes up through (2, 2) with an arrow instead of an endpoint.

Which piecewise function is shown in the graph?

f(x) = StartLayout enlarged left-brace 1st Row 1st column negative 0.5 x + 1, 2nd column x less-than 0 2nd row 1st column 2 x minus 2, 2nd column x greater-than-or-equal-to 0 EndLayout
f(x) = StartLayout enlarged left-brace 1st Row 1st column negative x + 1, 2nd column x less-than 0 2nd row 1st column 0.5 x minus 2, 2nd column x greater-than 0 EndLayout
f(x) = StartLayout enlarged left-brace 1st Row 1st column x minus 1, 2nd column x less-than-or-equal-to 0 2nd row 1st column 2 x minus 2, 2nd column x greater-than 0 EndLayout
f(x) = StartLayout enlarged left-brace 1st Row 1st column negative 0.5 x minus 1, 2nd column x less-than-or-equal-to 0 2nd row 1st column 2 x minus 2, 2nd column x greater-than-or-equal-to 0 EndLayout

Answer 1

The piecewise function described in the details for the graph corresponds with the first option

`f(x) = \left\{\begin{matrix}-0.5\cdot x + 1, & x < 0 \\2\cdot x -2, & x \geq 0 \\\end{matrix}\right.`

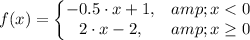
The steps used to find the piecewise function in the graph described can be presented as follows;

The coordinate points on the first line of the piecewise function indicates that we get;

The slope of the line, m, is; (3 - 1)/(-4 - 0) = -0.5

The y-intercept of the line is; (0, 1)

The equation of the line is therefore; f(x) = -0.5·x + 1 for x < 0

The coordinate points on the second line of the piecewise function indicates that we get;

The slope of the line, m, is; (2 - (-2))/(2 - 0) = 2

The y-intercept of the line is; (0, -2)

The equation of the line is therefore; f(x) = 2·x - 2 for x ≥ 0

The correct option is therefore;

`f(x) = \left\{\begin{matrix}-0.5\cdot x + 1, & x < 0\\2\cdot x-2, & \ x\geq 0\end{matrix}\right.`

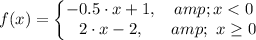
The above piecewise function corresponds with the first option