Question

Find m
45 ,45 ,√3 mi
Write your answer in simplest radical form
​

Answer 1

The length of each leg (m) is √1.5 miles.

We know the following:

The triangle is a right triangle because one of the angles is marked as 90 degrees.

The triangle is isosceles because two of the angles are marked as 45 degrees. In an isosceles triangle, two of the angles are always congruent.

The length of the hypotenuse is √3 miles because it is marked on the diagram.

We want to find the length of the legs, which are equal in an isosceles triangle and labeled as m in the diagram.

To find the length of the legs, we can use the Pythagorean theorem. The Pythagorean theorem states that in a right triangle, the square of the hypotenuse (c) is equal to the sum of the squares of the legs (a and b). In this case, we can write the equation as:

`c^2 = a^2 + b^2`

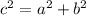
We know that c = √3 miles and a = b (because the legs are equal in an isosceles triangle). Substituting these values into the equation, we get:

`(\sqrt[]{3 miles} )^2 = a^2 + a^2`

Simplifying the equation, we get:

`3 miles^2 = 2a^2`

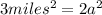
Dividing both sides by 2, we get:

`a^2 = 1.5 miles^2`

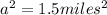
Taking the square root of both sides, we get:

a = b = √1.5 miles

Therefore, the length of each leg (m) is √1.5 miles.