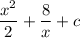The integral expression
![\int\limits {[x + 8\ln(x)]} \, dx](https://img.qammunity.org/2024/formulas/mathematics/college/39oocyag2abdr5pcy7uodv1717sdosgsy0.png) when evaluated is
when evaluated is
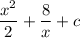
How to evaluate the integral expression
From the question, we have the following parameters that can be used in our computation:
![\int\limits {[x + 8\ln(x)]} \, dx](https://img.qammunity.org/2024/formulas/mathematics/college/39oocyag2abdr5pcy7uodv1717sdosgsy0.png)
This can be expanded as
![\int\limits {[x + 8\ln(x)]} \, dx = \int\limits x dx + \int\limits 8\ln(x) \, dx](https://img.qammunity.org/2024/formulas/mathematics/college/999n8v59cqt5xs3hktz0m38hs228jw667y.png)
Integrat each part
So, we have
![\int\limits {[x + 8\ln(x)]} \, dx = (x^2)/(2) + (8)/(x) + c](https://img.qammunity.org/2024/formulas/mathematics/college/z1xr9kdmjbugwvq89v2uhl9u9aiz3n6b4n.png)
Hence, the integral expression when evaluated is