Question

Given the graph what is the equation of the line that is perpendicular to the given line and passes through the point (4,-5)

Answer 1

The equation of the line perpendicular to the given line with slope 3 that passes through (4,-5) is y = -1/3x - 5, derived from the negative reciprocal of the given line's slope and using the point-slope formula.

To find the equation of a line that is perpendicular to a given line and passes through a specific point (4,-5), you have to use the negative reciprocal of the original line's slope. The given line has a slope (m) of 3. Therefore, the slope of the perpendicular line will be -1/3, because the product of the slopes of two perpendicular lines is -1 (m1 * m2 = -1).

Using the point-slope form of a line's equation, which is y - y1 = m(x - x1), where (x1,y1) is a point on the line (4, -5 in this case) and m is the slope (-1/3), we plug in our values:

`y - (-5) = (-1)/(3(x - 4))`

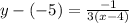
This simplifies to:

`y + 5 = (-1)/(3x) + (4)/(3)`

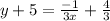
Subtracting 5 from both sides gives us the final equation of the line in slope-intercept form:

`y = (-1)/(3x) - (15)/(3)`

`y = (-1)/(3x) - 5`

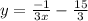
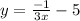
This is the equation of the line that is perpendicular to the given line and passes through the point (4,-5).