Question

A tennis ball is thrown straight up with an initial speed of 22.5 m/s. If it is caught at the same distance above the ground, how high does the ball rise, and how long does it remain in the air?

Answer 1

1. The height to which the ball rise in the air is 25.8 m

2. The time spent by the ball in the air is 4.6 s

How to calculate the height to which the ball rise and the time spent in air?

1. The height to which the ball rise can be calculated as follow:

• Initial speed of the ball into the air = 22.5 m/s
• Acceleration due to gravity (g) = 9.81 m/s²
• Final velocity of ball in air (v) = 0 m/s (at highest point)
• Height to which the ball rise (h) =?

`h = (u^2)/(2g) \\\\h = (22.5^2)/(2\ *\ 9.8) \\\\h = 25.8\ m`

Thus, the height is 25.8 m

2. The time spent by the ball in the air can be calculated as follow:

• Height to which the ball rise (h) = 25.8 m
• Acceleration due to gravity (g) = 9.81 m/s²
• Time spent in air (T) =?

`T = \sqrt{(8h)/(g)} \\\\T = \sqrt{(8\ *\ 25.8)/(9.8)} \\\\T = 4.6\ s`

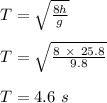
Thus, the ball will spend 4.6 s in the air