Final Answer:
The relationship between the image distance (
) and the object distance (
) for a plane (flat) mirror is that they are equal in magnitude but opposite in direction. In other words, (
).
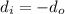Step-by-step explanation:
When an object is placed in front of a plane mirror, light rays from the object reflect off the mirror's surface. The reflected rays appear to originate from behind the mirror. The image formed is virtual, meaning it cannot be projected onto a screen. To understand the relationship between the object and image distances, consider the mirror equation:
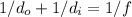
where
is the focal length of the mirror. For a plane mirror,
is considered infinite, so the equation simplifies to
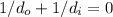Rearranging this equation yields
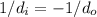which shows that the image distance (
) is equal in magnitude but opposite in sign to the object distance (
).
Therefore, if an object is placed \(10\) cm in front of a plane mirror, the image will appear \(10\) cm behind the mirror. This relationship holds true regardless of the object's distance from the mirror, as the image formed is virtual and located behind the mirror at an equal distance to the object in front. Consequently, the ratio of image distance to object distance remains \(1:1\) in magnitude but with opposite signs, demonstrating the consistent relationship between them in a plane mirror setup.