Question

Find the missing side length of the right triangle. round to the nearest tenth

Answer 1

Answer:Rounded to the Nearest tenth: 15.2

Explanation:

To solve for this side, we can use the Pythagorean Theorem (a^2+b^2=c^2)

As the side opposite of the Right Angle would be the Hypotenuse (c^2), you would set it equal to 256

5^2 is 25 so you would subtract 25 from the 256. Then you would take the square root of 231 to find your missing side length.

Answer 2

`\sf x= 15.2`

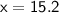
Explanation:

To find the missing side length (perpendicular) of the right triangle, we can use the Pythagorean Theorem.

The Pythagorean Theorem states that "in a right-angled triangle, the square of the length of the hypotenuse (c) is equal to the sum of the squares of the lengths of the other two sides (a and b)".

The formula is given by:

`\sf c^2 = a^2 + b^2`

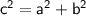
In this case:

• Hypotenuse (c) = 16
• Base (a) = 5
• Perpendicular (b) = x

Substitute these values into the Pythagorean Theorem:

`\sf 16^2 = 5^2 + x^2`

`\sf 256 = 25 + x^2`

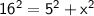
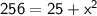
Now, solve for x:

`\sf x^2 = 256 - 25`

`\sf x^2 = 231`

`\sf x = √(231)`

`\sf x \approx 15.19868415`

`\sf x \approx 15.2 \textsf{(in nearest tenth})`

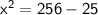
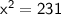
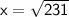
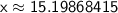
So, the missing side length x = 15.2, rounded to the nearest tenth.