Question

Salmon often jump waterfalls to reach their breeding grounds. Starting 2.00 m from a waterfall 0.55 m in height, at what minimum speed must a salmon jumping at an angle of 32 degrees leave the water to continue upstream?

Answer 1

The minimum speed the salmon must jump in order to continue upstream is 6.2 m/s

How to calculate the minimum speed of the salmon?

The minimum speed the salmon must jump can be calculated as illustrated below:

• Maximum height (H) = 0.55 m
• Angle of projection (θ) = 32 degrees
• Acceleration due to gravity (g) = 9.8 m/s²
• Minimum speed of salmon (u) = ?

Maximum height is given by:

`H = (u^2Sine^(2)\theta)/(2g)`

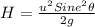
Input the given parameters to find u

`H = (u^2Sine^(2)\theta)/(2g)\\\\0.55 = (u^2(Sine\ 32)^(2))/(2\ *\ 9.8)\\\\Cross\ multiply\\\\u^2(Sine\ 32)^(2) = 0.55\ *\ 2\ *\ 9.8\\\\Divide\ both\ sides\ by\ (Sine\ 32)^(2)\\\\u^2 = (0.55\ *\ 2\ *\ 9.8)/((Sine\ 32)^(2)) \\\\u = \sqrt{(0.55\ *\ 2\ *\ 9.8)/((Sine\ 32)^(2))} \\\\u = 6.2\ m/s`

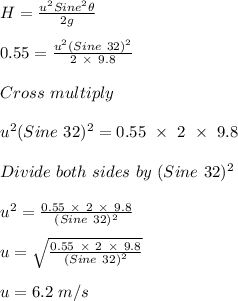
From the above, we can say that the salmon must jump with a minimum speed of 6.2 m/s if it must continue upstream