Question

A radio tower's signal covers a circular area with a radius r in miles.

The strength of the signal is increased, and now covers an area of
π² + 12πr + 36π square miles. By how much did the radius of the
coverage area increase?

Answer 1

`\[ r_2 = 6 + √(\pi + 72) \]` The radius increased by
`\( √(\pi + 72) \)` miles.

Let's denote the initial radius as
`\(r_1\)` and the increased radius as
`\(r_2\)`. The formula for the area of a circle is
`\(A = \pi r^2\)`. The increased area is given as
`\(\pi^2 + 12\pi r + 36\pi\)`. So, we have:

`\[A_1 = \pi r_1^2\]`

`\[A_2 = \pi^2 + 12\pi r_2 + 36\pi\]`

The increase in the area is given by:

`\[ \Delta A = A_2 - A_1 \]`

Substituting the area formulas:

`\[ \Delta A = (\pi^2 + 12\pi r_2 + 36\pi) - (\pi r_1^2) \]`

To find the increase in radius, we set
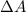`\(\Delta A\)` equal to the area formula for a circle:

`\[ \pi r_2^2 - \pi r_1^2 = \pi^2 + 12\pi r_2 + 36\pi - \pi r_1^2 \]`

Solving for
`\(r_2\)`:

`\[ r_2^2 - r_1^2 = \pi + 12r_2 + 36 \]`

Rearranging:

`\[ r_2^2 - 12r_2 = \pi + 36 \]`

Completing the square:

`\[ (r_2 - 6)^2 = \pi + 36 + 36 \]`

`\[ (r_2 - 6)^2 = \pi + 72 \]`

`\[ r_2 - 6 = √(\pi + 72) \]`

Finally, solving for
`\(r_2\)`:

`\[ r_2 = 6 + √(\pi + 72) \]`