Question

The blob doubles in volume every 23 minutes how long would it take from 5l to 60l

Answer 1

The calculated time to reach 60 l from 5l is 81.6 minutes

How to determine the time to reach 60 l from 5l

From the question, we have the following parameters that can be used in our computation:

Initial, P(0) = 5l

Final, P(t) = 60l

Doubling time, d = 23 minutes

Express time in hour

So, we have

d = 23/60

The time to reach 60 l from 5l can be calculated using

`P_t = P_0 \cdot 2^(t)/(d)`

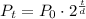
Substitute the known values into the equation

`60 = 5 \cdot 2^(t)/(23/60)`

`12 = 2^(t)/(23/60)`

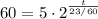
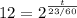
Evaluate the quotient of 23 and 60

`12 = 2^(t)/(0.38)`

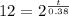
Take the logarithm of both sides

`\log(12) = \log(2)^(t)/(0.38)`

This means that

`\log(12) = (t)/(0.38)\log(2)`

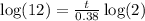
So, we have

`(t)/(0.38) = (\log(12))/(\log(2))`

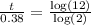
Multiply through by 0.38

`t = (\log(12))/(\log(2)) * 0.38`

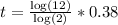
Evaluate

t = 1.36

Convert to minutes

t = 1.36 * 60

t = 81.6

hence, the time to reach 60 l from 5l is 81.6 minutes