Question

If f(c) 1-2c 2c+1 when c # -1/2 then find f(-1/c)​

Answer 1

The expression that represents the function f(-1/c)​ is
`\text{f(-1/c)}= (c + 2)/(c - 2)`

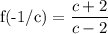
How to evaluate the function

From the question, we have the following parameters that can be used in our computation:

`\text{f(c)} = (1 - 2c)/(2c + 1)`

To calculate f(-1/c)​, we replace c with -1/c

Using the above as a guide, we have the following:

`\text{f(-1/c)} = (1 - 2 * -1/c)/(2 * -1/c + 1)`

Evaluate the products, we have

`\text{f(-1/c)} = (1 + 2/c)/(-2/c + 1)`

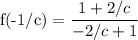
Take the LCM

`\text{f(-1/c)}= ((c + 2)/c)/((-2 + c)/c)`

Simplify the quotient

`\text{f(-1/c)} = (c + 2)/(-2 + c)`

Rewrite as

`\text{f(-1/c)}= (c + 2)/(c - 2)`

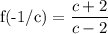
Hence, the expression that represents the function is
`\text{f(-1/c)}= (c + 2)/(c - 2)`

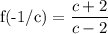
Question

If
`\text{f(c)} = (1 - 2c)/(2c + 1)` when c ≠ -1/2 then find f(-1/c)​