1.
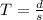 : The unknown variable
: The unknown variable
 .
.
2.
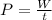 : The unknown variable
: The unknown variable
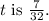
3.
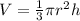 : The unknown variable
: The unknown variable
 .
.
4.
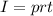 : The unknown variable
: The unknown variable
 .
.
Let's substitute the given values into each formula and solve for the unknown variable.
1. Formula:
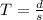
- Given values:
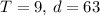
- Substitute and solve:
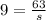
- Solve for
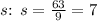
So, the unknown variable
 .
.
2. Formula:
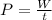
- Given values:

- Substitute and solve:
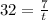
- Solve for
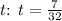
So, the unknown variable
 .
.
3. Formula:
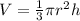
- Given values:
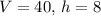
- Substitute and solve:
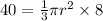
- Solve for
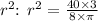
- Solve for

So, the unknown variable
 .
.
4. Formula:
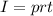
- Given values:
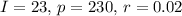
- Substitute and solve:
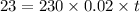
- Solve for
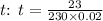
So, the unknown variable
 .
.