The measure of m∠ABD is given as C)Using the Angle Addition Postulate, 40 + m∠ABD = 70. So, m∠ABD = 30° using the subtraction property of equality
How to get the angle
Angle Addition Postulate states that the sum of the measures of two adjacent angles is equal to the measure of the angle formed by the non-common sides of the two adjacent angles.
Given that angles ADB and DBC are adjacent angles, and the sum of these two adjacent angles is equal to angle ABC:
Using the Angle Addition Postulate:
![\[ \angle ABC = \angle ABD + \angle DBC \]](https://img.qammunity.org/2024/formulas/mathematics/college/j6ldd9ij3pyu5bssulg5ydnlu0263wkmxj.png)
Given:
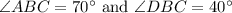
![\[ 70^\circ = \angle ABD + 40^\circ \]](https://img.qammunity.org/2024/formulas/mathematics/college/70z0zt1bglaq9wgmzuab8mvmm5s5mj64wz.png)
To find the measure of \(\angle ABD\):
![\[ \angle ABD = 70^\circ - 40^\circ \]\\\[ \angle ABD = 30^\circ \]](https://img.qammunity.org/2024/formulas/mathematics/college/f8d1ssbejvv1zz0hmcanv2qk3dcy5a23xz.png)
Therefore, the measure of angle ABD is
Question
If m∠ABC = 70°, what is m∠ABD? Justify your reasoning. A)Using the addition property of equality, 40 + 70 = 110, so m∠ABD = 110°. B)Using the subtraction property of equality, 70 − 30 = 40, so m∠ABD = 30°. C)Using the Angle Addition Postulate, 40 + m∠ABD = 70. So, m∠ABD = 30° using the subtraction property of equality. D) Using the Angle Addition Postulate, 40 + 70 = m∠ABD. So, m∠ABD = 110° using the addition property of equality.