Answer:
1)

2)

3) Sidewalk 1 has a steeper slope.
Explanation:
Part (1)
Equation for Sidewalk 1 in Slope-Intercept Form:
To find the equation in slope-intercept form (
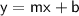 ), where
), where
 is the slope and
is the slope and
 is the y-intercept, we can use the given points
is the y-intercept, we can use the given points
 and
and
 .
.
First, find the slope (
 ):
):

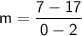
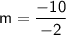

Now that we have the slope, choose one of the points (let's use
 ) and substitute into the slope-intercept form equation:
) and substitute into the slope-intercept form equation:
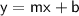
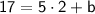

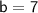
So, the equation for Sidewalk 1 is
 in slope-intercept form.
in slope-intercept form.

Part (2) Equation for Sidewalk 2 in Point-Slope Form:
To find the equation in point-slope form (
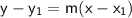 ), where
), where
 is a point on the line and
is a point on the line and
 is the slope, we can use the given points
is the slope, we can use the given points
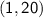 and
and
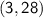 .
.
First, find the slope (
 ):
):

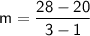

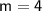
Now, choose one of the points (let's use
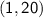 ) and substitute into the point-slope form equation:
) and substitute into the point-slope form equation:
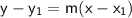
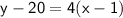
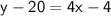

So, the equation for Sidewalk 2 is
 in point-slope form.
in point-slope form.

(3) Identify which sidewalk has a steeper slope:
The slopes of the two sidewalks are as follows:
- Sidewalk 1:

- Sidewalk 2:
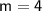
Sidewalk 1 has a steeper slope (5) compared to Sidewalk 2 (4).