Question

A certain culture of the bacterium Rhodobacter sphaeroides initially has 50 bacteria and is observed to double every 5 hours.

(a) The exponential model is n(t)=50(2)^(t/5) (already solved)
(b) Estimate the number of bacteria after 13 hours. (Round your answer to the nearest whole number.)
(c) After how many hours will the bacteria count reach 1 million? (Round your answer to one decimal place.)

Answer 1

The number of bacteria after 13 hours is 303.14

The bacteria culture will reach 1 million in 71.5 hours

Estimating the number of bacteria after 13 hours

From the question, we have the following parameters that can be used in our computation:

`n(t) = 50 \cdot (2)^\frac t5`

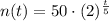
After 13 hours, we have

t = 13

Substitute the known values into the equation

`n(13) = 50 \cdot (2)^\frac {13}5`

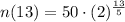
Evaluate

n(13) = 303.14

So, the population after 13 hours is 303.14

When the bacteria count reaches 1 million, we have

`50 \cdot (2)^\frac t5 = 1000000`

Divide through by 50

`(2)^\frac t5 = 20000`

Take the logarithm of both sides

`\frac t5 = (\log(20000))/(\log(2))`

`\frac t5 = 14.3`

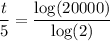
t = 14.3 * 5

t = 71.5

Hence, it will reach 1 million in 71.5 hours