Question

Una máquina lanza un proyectil a una velocidad de 110m/s con ángulo de 35 calcular

Altura Max
Tiempo en la max altura
Tiempo total del vuelo
Alcance logrado

Answer 1

Projectile launched at 110 m/s, 35° angle. Max height: 203.06 m, time to max height: 6.45 s, total flight time: 12.90 s, horizontal range: 1162.72 m.

To solve these problems, we can use the kinematic equations of motion for projectile motion. The initial velocity \(v_0\) can be decomposed into horizonta
`l (\(v_(0x)\)) and vertical (\(v_(0y)\))`components using trigonometric functions. The acceleration in the vertical direction
`(\(a_y\)) is usually taken as the gravitational acceleration (\(g\)), which is approximately \(9.8 \ \text{m/s}^2\)` on the surface of the Earth.

1. **Maximum Height (\(H\)):**

- The formula for the maximum height is given by:

`\[ H = \frac{{v_(0y)^2}}{{2g}} \]`

2. **Time to Reach Maximum Height
`(\(t_{\text{max}})\):**`

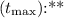
- The time it takes to reach the maximum height is given by:

`\[ t_{\text{max}} = \frac{{v_(0y)}}{{g}} \]`

3. **Total Time of Flight (\(T\)):**

- The total time of flight is twice the time to reach the maximum height:

`\[ T = 2 * t_{\text{max}} \]`

4. **Horizontal Range (\(R\)):**

- The horizontal range is given by:

`\[ R = v_(0x) * T \]`

Let's calculate these values using the given information:

Given:

`- Initial velocity (\(v_0\)) = \(110 \ \text{m/s}\)`

`- Launch angle (\(\theta\)) = \(35^\circ\)`

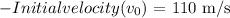
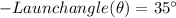
First, we decompose the initial velocity into horizontal and vertical components:

`\[ v_(0x) = v_0 * \cos(\theta) \]\[ v_(0y) = v_0 * \sin(\theta) \]`

Now, let's calculate:

`\[ v_(0x) = 110 \ \text{m/s} * \cos(35^\circ) \]\[ v_(0y) = 110 \ \text{m/s} * \sin(35^\circ) \]\[ g = 9.8 \ \text{m/s}^2 \]`

1. **Maximum Height (\(H\)):**

`\[ H = \frac{{v_(0y)^2}}{{2g}} \]`

2. **Time to Reach Maximum Height (\(t_{\text{max}})\):**

`\[ t_{\text{max}} = \frac{{v_(0y)}}{{g}} \]`

3. **Total Time of Flight (\(T\)):**

`\[ T = 2 * t_{\text{max}} \]`

4. **Horizontal Range (\(R\)):**

`\[ R = v_(0x) * T \]`

Let's calculate these values.

`\[ v_(0x) = 110 \ \text{m/s} * \cos(35^\circ) \approx 90.16 \ \text{m/s} \]`

`\[ v_(0y) = 110 \ \text{m/s} * \sin(35^\circ) \approx 63.15 \ \text{m/s} \]`

`\[ g = 9.8 \ \text{m/s}^2 \]`

1. **Maximum Height (\(H\)):**

`\[ H = \frac{{v_(0y)^2}}{{2g}} \]`

`\[ H = \frac{{63.15^2}}{{2 * 9.8}} \approx 203.06 \ \text{m} \]`

2. **Time to Reach Maximum Height (\(t_{\text{max}})\):**

`\[ t_{\text{max}} = \frac{{v_(0y)}}{{g}} \]`

`\[ t_{\text{max}} = \frac{{63.15}}{{9.8}} \approx 6.45 \ \text{s} \]`

3. **Total Time of Flight (\(T\)):**

`\[ T = 2 * t_{\text{max}} \]`

`\[ T = 2 * 6.45 \approx 12.90 \ \text{s} \]`

4. **Horizontal Range (\(R\)):**

`\[ R = v_(0x) * T \]`

`\[ R = 90.16 \ \text{m/s} * 12.90 \ \text{s} \approx 1162.72 \ \text{m} \]`

So, the answers are:

1. Maximum Height (\(H\)) ≈ 203.06 m

2. Time to Reach Maximum Height (\(t_{\text{max}}\)) ≈ 6.45 s

3. Total Time of Flight (\(T\)) ≈ 12.90 s

4. Horizontal Range (\(R\)) ≈ 1162.72 m