To find the equation of a line parallel to
 and passing through the point
and passing through the point
 , we can use the fact that parallel lines have the same slope. The given line
, we can use the fact that parallel lines have the same slope. The given line
 has a slope
has a slope
 of -3.
of -3.
Now, using the point-slope form of the equation
 , where
, where
 is a point on the line and
is a point on the line and
 is the slope, substitute the values:
is the slope, substitute the values:
![\[(y - (-4)) = -3(x - (-2))\]](https://img.qammunity.org/2024/formulas/mathematics/college/2jhv5dew9fn54qai6tqdhmkz72g9d5hr29.png)
Simplify the equation:
![\[y = -3x - 10\]](https://img.qammunity.org/2024/formulas/mathematics/college/zs14nrp524tqrcu7f11ggubfptbmgjdwl8.png)
Now, convert it to the slope-intercept form
 :
:
![\[y = -3x - 10\]](https://img.qammunity.org/2024/formulas/mathematics/college/zs14nrp524tqrcu7f11ggubfptbmgjdwl8.png)
So, the slope-intercept form of the equation for the line parallel to
 and passing through
and passing through
 is
is
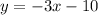 .
.