Question

Evaluate the definite and indefinite integral given below.

Answer 1

`\text{22) }(1)/(24)(4x+7)^6+C`

23) upper bound = 14 and lower bound = -56

Explanation:

For question 22 we are asked to evaluate the following indefinite integral:

`\displaystyle \int {(4x+7)^5} \, dx`

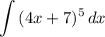
For question 23 we are asked to apply u-substitution and determine the new upper and lower bounds for the following definite integral:

`\displaystyle \int\limits^2_(-3) {2x^2(2x^3-2)^5} \, dx`

`\hrulefill`

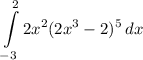
Question 22
`\hrulefill`

To evaluate the following:

`\displaystyle \Longrightarrow \int {(4x+7)^5} \, dx`

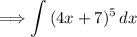
Apply u-substitution, let u = 4x + 7 and du = 4dx. Substituting these values in we have:

`\displaystyle \Longrightarrow \int {(u)^5} \, (du)/(4)`

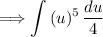
We can pull out the constant:

`\displaystyle \Longrightarrow (1)/(4) \int {u^5} \, du`

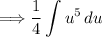
Now we have a simple power rule, lets integrate:

`\boxed{\left\begin{array}{ccc}\text{\underline{Power Rule:}}\\\\\displaystyle \int x^n \, dx = (x^(n+1))/(n+1)\end{array}\right}`

`\displaystyle \Longrightarrow (1)/(4) \Big[(u^(5+1)+C)/(5+1)\Big]\\\\\\\\\\\displaystyle \Longrightarrow (1)/(4) \Big[(u^(6))/(6)+C\Big]\\\\\\\\\Longrightarrow (1)/(24)u^6+C`

Now plug in '4x + 7' back in for 'u'


`\therefore \displaystyle \int {(4x+7)^5} \, dx = \boxed{(1)/(24)(4x+7)^6+C}`

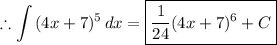
Thus, the answer is found. 'C' is the constant of integration.

`\hrulefill`

Question 23
`\hrulefill`

We have the following:

`\displaystyle \int\limits^2_(-3) {2x^2(2x^3-2)^5} \, dx`

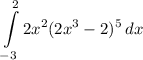
Applying u-substitution. Let u = 2x³ - 2, then du = 6x²dx. Plugging these in we get:

`\Longrightarrow \displaystyle \int\limits^(u_u)_(u_l) {2x^2(u)^5} \, (du)/(6x^2)\\\\\\\\\Longrightarrow \displaystyle (1)/(3)\int\limits^(u_u)_(u_l) {u^5} \, du`

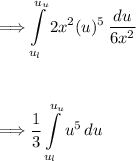
Since the integrand was changed, we will have different upper and lower bounds. We can use the fact that u = 2x³ - 2 to find our new limits.

For the upper bound, x = 2:

⇒ u = 2x³ - 2

⇒ u = 2(2)³ - 2

⇒ u = 2(8) - 2

⇒ u = 16 - 2

∴ u_upper = 14

For the upper bound, x = -3:

⇒ u = 2x³ - 2

⇒ u = 2(-3)³ - 2

⇒ u = 2(-27) - 2

⇒ u = -54 - 2

∴ u_upper = -56

Thus, our new bounds have been found. The integral will look like this:

`\Longrightarrow \displaystyle (1)/(3)\int\limits^(15)_(-56) {u^5} \, du`

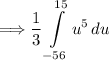
We can then integrate the above without having to substitute '2x³ - 2' back in for 'u'. This is because the integral is entirely in terms of 'u' now.