Question

Evaluate the definite integral given below.
`\int _0^{(\pi )/(4)}\:\left(3sin\left(x\right)-2cos\left(x\right)\right)dx`Enter an exact answer. Provide your answer below:

Answer 1

Answer:
`(-5√(2))/(2)+3`

Work Shown

`\displaystyle \int_(0)^{(\pi)/(4)} \left(3\sin(\text{x})-2\cos(\text{x})\right)d\text{x}\\\\\\= -3\cos(\text{x})-2\sin(\text{x})\bigg|_(0)^{(\pi)/(4)}\\\\\\= \left(-3\cos\left((\pi)/(4)\right)-2\sin\left((\pi)/(4)\right)\right)-\left(-3\cos(0)-2\sin(0)\right)\\\\\\`

`= \left(-3*(√(2))/(2)-2*(√(2))/(2)\right)-\left(-3*1-2*0\right)\\\\\\= \left((-3√(2))/(2)+(-2√(2))/(2)\right)-\left(-3-0\right)\\\\\\= (-3√(2)-2√(2))/(2)+3\\\\\\= (-5√(2))/(2)+3\\\\\\`

Therefore,

`\displaystyle \int_(0)^{(\pi)/(4)} \left(3\sin(\text{x})-2\cos(\text{x})\right)d\text{x}= (-5√(2))/(2)+3\\\\\\`

Notes:

• We don't have to worry about the plus C because we're working with definite integrals.
• The answer shown above approximates to roughly -0.5355
• Use the unit circle to evaluate sin(pi/4) and cos(pi/4).

Answer 2

`3-(5 √(2))/(2)`

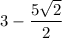
Explanation:

We are given the following definite integral:

`\displaystyle \int\limits^{(\pi)/(4)}_0 {(3 \sin(x) - 2 \cos(x))} \, dx`

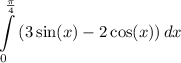
We are asked to evaluate it and leave the answer in exact form.

Basic Integration Rules:

`\boxed{ \left \begin{array}{ccc} \text{\underline{Basic Integration Rules:}} \\\\ 1. \ \int c \, dx = cx \\\\ 2. \ \int cf(x) \, dx = c \int f(x) \, dx \\\\ 3. \ \int [f(x) \pm g(x)] \, dx = \int f(x) \, dx \pm \int g(x) \, dx \\\\ 4. \ \int x^n \, dx = (x^(n+1))/(n+1) \ \text{(Power rule, for } n \\eq -1) \\\\ \text{Where:} \\ \bullet \ c \ \text{is a constant} \\ \end{array} \right.}`

Basic Trigonometric Integration Rules:

`\boxed{ \left \begin{array}{ccc} \text{\underline{Trigonometric Integral Rules:}} \\\\ 1. \ \int \sin(x) \, dx = -\cos(x) \\\\ 2. \ \int \cos(x) \, dx = \sin(x) \\\\ 3. \ \int \tan(x) \, dx = -\ln|\cos(x)| \\\\ 4. \ \int \cot(x) \, dx = \ln|\sin(x)| \\\\ 5. \ \int \sec(x) \, dx = \ln|\sec(x) + \tan(x)| \\\\ 6. \ \int \csc(x) \, dx = -\ln|\csc(x) + \cot(x)| \\\\ \end{array} \right.}`

`\hrulefill`

Now solving, lets apply some of the basic integration rules. Apply (3) to split up the integral and (4) to pull out the constants:

`\displaystyle \Longrightarrow \int\limits^{(\pi)/(4)}_0 {(3 \sin(x) - 2 \cos(x))} \, dx\\\\\\\\\Longrightarrow \int\limits^{(\pi)/(4)}_0 {3 \sin(x)} \, dx - \int\limits^{(\pi)/(4)}_0 {2 \cos(x)} \, dx\\\\\\\\\Longrightarrow 3\int\limits^{(\pi)/(4)}_0 {\sin(x)} \, dx - 2\int\limits^{(\pi)/(4)}_0 {\cos(x)} \, dx`

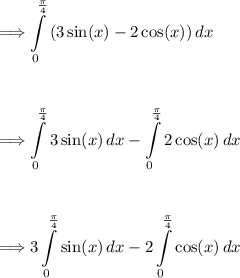
Now we have basic sine and cosine trig rules, apply them accordingly:

`\Longrightarrow 3\Big[-\cos(x)\Big]^{(\pi)/(4)}_0 - 2\Big[\sin(x)\Big]^{(\pi)/(4)}_0`

Let's rewrite:

`\Longrightarrow \Big[-3\cos(x)\Big]^{(\pi)/(4)}_0 - \Big[2\sin(x)\Big]^{(\pi)/(4)}_0\\\\\\\\\Longrightarrow \Big[-3\cos(x)-2\sin(x)\Big]^{(\pi)/(4)}_0`

Now evaluate at the given bounds:

`\Longrightarrow \Big[-3\cos\left((\pi)/(4)\right)-2\sin\left((\pi)/(4)\right)\Big]-\Big[-3\cos(0)-2\sin(0)\Big]`

Using the unit circle (attached as image) we can determine the values of the trig functions:

`\Longrightarrow \Big[-3\left((\sqrt2)/(2)\right)-2\left((\sqrt2)/(2)\right)\Big]-\Big[-3(1)-2(0)\Big]\\\\\\\\\Longrightarrow \Big[(-3\sqrt2)/(2)\right)-\sqrt2\right)\Big]-\Big[-3\Big]\\\\\\\\\Longrightarrow (-3\sqrt2)/(2)\right)-\sqrt2+3\\\\\\\\\Longrightarrow (-3\sqrt2)/(2)\right)-(\sqrt2)/(1)+3\\\\\\\\\Longrightarrow (-3\sqrt2)/(2)\right)-(2\sqrt2)/(2)+3\\\\\\\\`

`\displaystyle \therefore \displaystyle \int\limits^{(\pi)/(4)}_0 {(3 \sin(x) - 2 \cos(x))} \, dx = \boxed{3-(5\sqrt2)/(2)}`

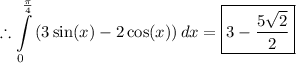
Thus, the problem is solved.