Question

Find all solutions to the equation x Superscript 4 Baseline minus 4 x cubed + 4 x squared + 4 x minus 5 = 0. The real solutions are . The nonreal solutions are .

Answer 1

The two real solutions of the equation x⁴ - 4x³ + 4x² + 4x - 5 = 0 are 1 and -1.

How to find the real solutions of the equation?

We have the cubic equation:

x⁴ - 4x³ + 4x² + 4x - 5 = 0

And we want to find the real solutions for this equation.

We can rewrite this as:

x⁴ + 4*(-x³ + x² + x) - 5 = 0

Notice that if x = 1, we have a solution, so x = 1 is a factor.

1⁴ + 4*(-1³ + 1² + 1) - 5 = 0

0 = 0

And also, x = -1 is also a solution

(-1)⁴ + 4*(-(-1)³ +(-1)² + (-1)) - 5 = 0

then we can write the polynomial as:

(x + 1)*(x - 1)*[ax² + bx + c] = x⁴ - 4x³ + 4x² + 4x - 5

Because a is on the quartic term, we know that a = 1

(x + 1)*(x - 1)*[x² + bx + c] = x⁴ - 4x³ + 4x² + 4x - 5

Then c*-1*1 = -5,

c = -5/-1 = 5

so:

(x + 1)*(x - 1)*[x² + bx + -5] = x⁴ - 4x³ + 4x² + 4x - 5

And for b we can write:

bx*x + b*x*x + x²*1 + x²*-1 = 4x²

2bx² = 4x²

2b = 4

b = 4/2

Then the equation becomes:

(x + 1)*(x - 1)*[x² + 2x + 5] = x⁴ - 4x³ + 4x² + 4x - 5

Now we need to find the roots of:

x² + 2x + 5

Using the quadratic formula we get:

`x = (-2 \pm √(2^4 - 4*5*1) )/(2) \\\\x = (-2 \pm √(-16) )/(2)`

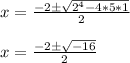
We have a negative argument in the square root, so the solutions are not real, and we can discard them.

The only real solutions are 1 and -1.