The formula for proving the properties of quadrilaterals are: 1. Midpoint formula:
 . 2. Distance formula:
. 2. Distance formula:
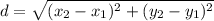 . 3.
. 3.
 =
=
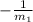 ; 4.
; 4.
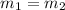 .
.
What are the formula used in proving the properties of quadrilaterals?
The properties that is used in proving the properties of a quadrilateral include the following as explained below:
Midpoint formula, which is given as:
 .
.
Distance formula, which is given as:
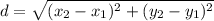 .
.
If opposite reciprocals, then the slope formula to use is:
 =
=
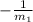 , where
, where
 and
and
 are the slopes of the two lines.
are the slopes of the two lines.
Where they are equal, the slope formula to use would be:
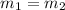 .
.