The electric field at a distance of 16 cm from the center of the conducting spherical shell, after the charge q has moved inside the shell, is zero. This is because inside the shell, the electric field is always zero, while outside the shell, the electric field can be calculated using Coulomb's law.
To calculate the electric field at a distance of 16 cm from the center of the conducting spherical shell, we need to consider the properties of the shell and the movement of the charge inside it.
Here's a step-by-step explanation:
1. Given information:
- Inner radius (a) = 5 cm
- Outer radius (b) = 10 cm
- Charge (q) = 1.3 nC
- Distance from the center of the shell (r) = 16 cm
2. The charge inside the shell:
Since the charge q is at the center of the shell, moving it inside the shell does not change the charge distribution. The total charge remains the same.
3. Electric field inside a conducting shell:
Inside a conducting shell, the electric field is always zero. This is because any electric field produced by the charge q is canceled out by the induced charges on the inner surface of the shell. Therefore, the electric field inside the shell is zero.
4. Electric field outside the shell:
To calculate the electric field outside the shell, we can use Coulomb's law, which states that the electric field (E) is equal to the charge (q) divided by the square of the distance (r) between the charge and the point where we want to calculate the field.
E = k * (q /
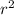 )
)
Where k is the electrostatic constant (k = 9 x
 ).
).
Plugging in the values:
E = (
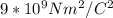 ) * (
) * (
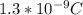 ) / (
) / (
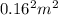 )
)
Calculating this equation will give us the electric field at a distance of 16 cm from the center of the shell.
The question probable may be:
A conducting spherical shell with inner radius a = 5 cm and outer radius b = 10 cm surrounds a charge q = 1.3 nC. The charge is at the center of the shell.
If the charge q moves inside the shell 2 cm to the right, what is the electric field at a distance of 16 cm from the center of the shell?