Question

asked Aug 17, 2024 105k views

1 Answer

Ole Wolf · Answer 1 · 2024-08-20T20:16:54+0000

The widths of the two frames are approximately 0.0709 inches for Frame A and 0.0632 inches for Frame B.

Let's denote the length and width of Frame A as
$L_A\) and $W_A$ respectively, and similarly
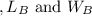$, \(L_B$ and $W_B$$ for Frame B.

The area
$($A$)$ of a rectangle is given by the formula
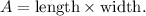
$$A = \text{length} * \text{width}$.$

For Frame A:

$A_A = L_A * W_A$

For Frame B:

$A_B = L_B * W_B$

Given that both frames have the same area of 45 square inches:

$A_A = A_B = 45$

You mentioned the length of Frame A
$($L_A$)$ is 634 inches, and the length of Frame B
$($L_B$)$ is 712 inches.

We can set up a system of equations to solve for the widths
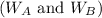$($W_A$ and $W_B$)$ :

$L_A * W_A = 45$

$L_B * W_B = 45$

Substitute the given lengths:

$634 * W_A = 45$

$712 * W_B = 45$

Now, solve for
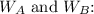
$$W_A$ and $W_B$:$

$W_A = (45)/(634)$

$W_B = (45)/(712)$

You can then calculate the values:

$W_A \approx 0.0709 \, \text{inches}$

$W_B \approx 0.0632 \, \text{inches}$

So, the widths of the two frames are approximately 0.0709 inches for Frame A and 0.0632 inches for Frame B.

Please log in or register to add a comment.