Question

Find the measure of Z1 in the figure, shown to the right.

m41-
12
34
81
7
M<1 ?°

Answer 1

The measure of
`\(\angle 1\)` in the given scenario is
`\(81^\circ\)`, following the congruence of corresponding angles when a line bisects two parallel lines.

When a line bisects two parallel lines, alternate interior angles are congruent. Given the information:

`\angle 1 & \text{ corresponds to } \angle 5 \text{ (given as } 81^\circ), \\`

`\angle 2 & \text{ corresponds to } \angle 6, \\`

`\angle 3 & \text{ corresponds to } \angle 7, \\`

`\angle 4 & \text{ corresponds to } \angle 8.\end{align*}`

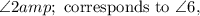
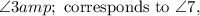
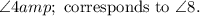
Since
`\(\angle 1\)` and
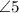`\(\angle 5\)` are corresponding angles, and
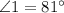`\(\angle 1 = 81^\circ\)`, we can conclude that
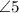`\(\angle 5\)` is also
`\(81^\circ\)`.

Thus,
`\(m(\angle 1) = m(\angle 5) = 81^\circ\)`.

In summary, when a line bisects two parallel lines, the measure of an angle formed by the bisector corresponds to the measure of the angle on the other side of the bisector. Therefore,
`\(m(\angle 1) = 81^\circ\)`.