Answer:
See attachment.
Explanation:
Given quadratic equation:
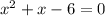
Therefore, the quadratic function is:
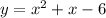
The graph of a quadratic function is a parabola.
- If the leading coefficient is positive, the parabola opens upwards.
- If the leading coefficient is negative, the parabola opens downwards.
Therefore, as the leading coefficient of the given quadratic function is positive, the parabola will open upwards.
x-intercepts
The x-intercepts are the points at which the curve crosses the x-axis, so when y = 0.
Therefore, to find the x-intercepts, factor the equation and solve for x:
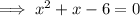
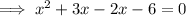
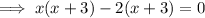
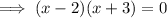
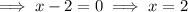
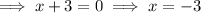
Therefore, the x-intercepts of the function are (2, 0) and (-3, 0).
Axis of symmetry
The axis of symmetry is the midpoint of the x-intercepts:
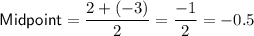
Therefore, the axis of symmetry of the function is x = -0.5.
Vertex
The axis of symmetry is the x-value of the vertex.
To find the y-value of the vertex, substitute the x-value into the function:

Therefore, the vertex of the function is (-0.5, -6.25).
y-intercept
The y-intercept is the point at which the curve crosses the y-axis, so when x = 0.
To find the y-intercept, substitute x = 0 into the function:
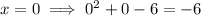
Therefore, the y-intercept of the function is (0, -6).
Graphing the function
To graph the function:
- Plot the vertex (-0.5, -6.25)
- Plot the x-intercepts (2, 0) and (-3, 0)
- Draw the axis of symmetry at x = -0.5
- Plot the y-intercept at (0, -6)
- Draw a curve symmetric about the axis of symmetry passing through the plotted points (upwards opening parabola).