The value of v that makes CDEF a parallelogram is 2. This is found by setting the lengths of opposite sides equal (CD = FE), and solving the resulting equation:
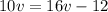 .
.
To determine the value of v that makes quadrilateral CDEF a parallelogram, we need to use the property that opposite sides of a parallelogram are equal in length.
Given:
![\[ CD = 10v \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/nrmii5a0qituevm1ceglmth91wfuorcksg.png)
![\[ FE = 16v - 12 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/zsz5n3upmyodjuoy7av45obofc2bov65rl.png)
For a parallelogram, opposite sides CD and FE must be equal:
![\[ 10v = 16v - 12 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/3uitnrhp7ot6x03ydg7e7xypa167mqnuay.png)
Now, solve for v:
![\[ 10v - 16v = -12 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/43p5zgp0rurwycp6gknakw3nbw516mqna9.png)
Combine like terms:
![\[ -6v = -12 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/4b30cnrbr9kc6tad0t3h9ywufhn5bnfoc0.png)
Divide by -6 to isolate v:
![\[ v = (-12)/(-6) = 2 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/yr0daahefynpmszrorxqo6cdcok6glc4a0.png)
So, the value of
 that makes quadrilateral CDEF a parallelogram is
that makes quadrilateral CDEF a parallelogram is
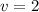 . If
. If
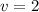 , then CD and FE are equal in length, satisfying the condition for opposite sides of a parallelogram.
, then CD and FE are equal in length, satisfying the condition for opposite sides of a parallelogram.